Nota: (tenemos esta practica de una Regresion-Lineal en TensorFlow-2.x para llevarla acabo usaremos Google-Collaboration, se ejecuta completamente en Cloud no requiere configuración y que ofrece acceso sin coste adicional a recursos informáticos, como Jupyter y GPUs).
Nota: (esta Herramienta Google-Collaboration tiene ciertas limitaciones; una sola GPU con memoria 12GB, la TPU proporciona 64GB de memoria y el tiempo de utilización 12-horas en forma continua no esta mal para ser gratis).
Que es Regresión-Linea: (es un Algoritmo-Aprendizaje-Supervisado que se utiliza en Machine-Learning y en estadística. En su versión más sinple, lo que haremos es dibujar una recta que nos indicará la tendencia de un conjunto de datos continuos, si fueran discretos, utilizaríamos Regresión Logística. En estadísticas, regresión lineal es una aproximación para modelar la relación entre una variable escalar dependiente “y” y una o mas variables explicativas nombradas con “X”).
Regresión-Lineal-TensorFlow-2.0
Nota: Entramos en Google-Collaboration en el cual tenemos que tener instalado TensorFlow-2.0.
Importamos las librerias:
- import tensorflow as tf
- import numpy as np
- import matplotlib.pyplot as plt
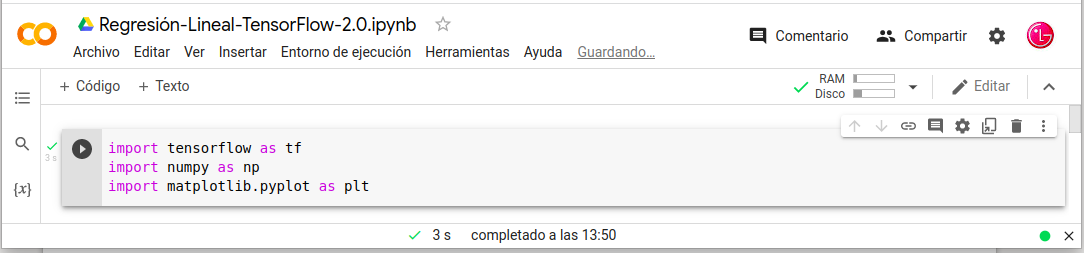
Definiremos el modelo de regresión lineal:
- class LinearModel(object):
- def __init__(self):
- self.W = tf.Variable(12.0)
- self.b = tf.Variable(-6.1)
- def __call__(self, inputs):
- return self.W * inputs + self.b
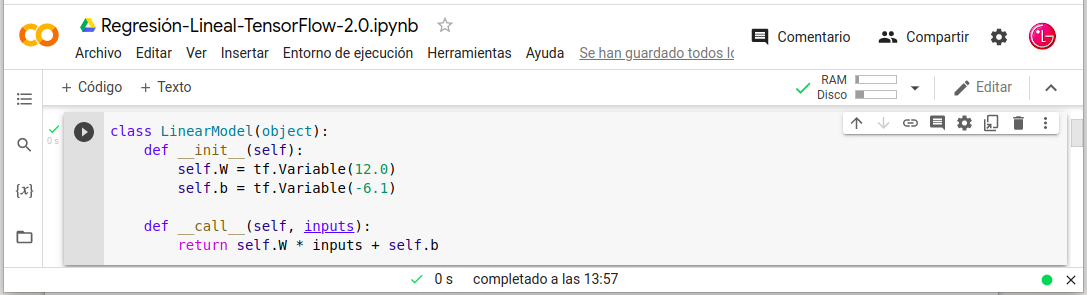
Nota: Definiremos la Función de Costo y lanzamos el Modelo.
Definiremos la función de costo del modelo:
- def compute_loss(y_true, y_pred):
- return tf.reduce_mean(tf.square(y_true-y_pred))
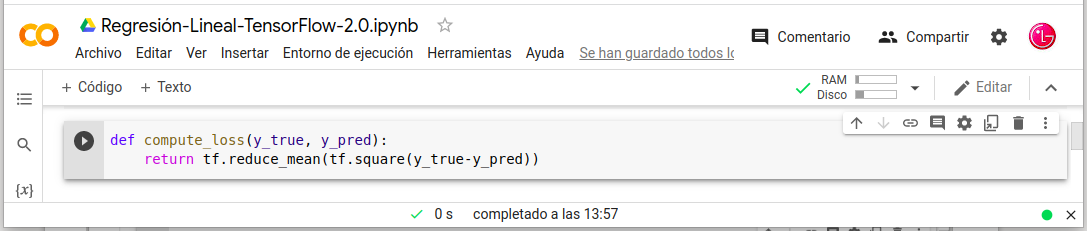
Inicializar el modelo:
- model = LinearModel()
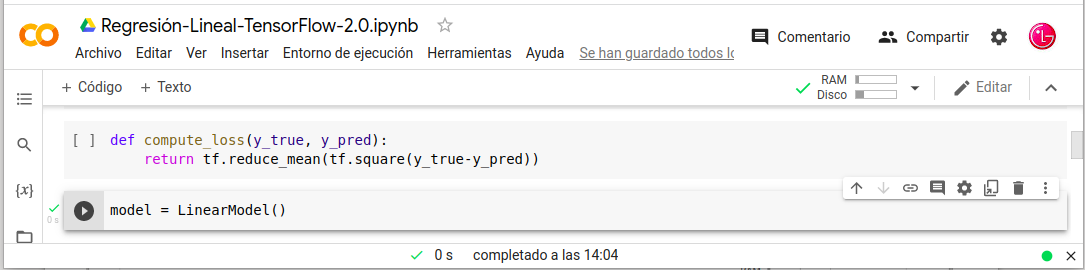
Nota: Definimos el Peso (weight) y Sesgo (bias) y los datos para entrenar el modelo.
Definimos Peso y el Sesgo:
- weight = 2.5
- bias = 1.0
Cargar los Datos para entrenar el modelo:
- data = 300
- inputs = tf.random.normal(shape=[data])
- noise = tf.random.normal(shape=[data])
- outputs = inputs * weight + bias + noise
Verificar los datos generados:
- print(inputs)
- print(noise)
- print(outputs)
Visualización–Datos-Durante el Entrenamiento:
- def plot(epoch):
- plt.scatter(inputs, outputs, c=’b’)
- plt.plot(inputs, model(inputs), c=‘r’, label =‘Fitted line’)
- plt.title(«epoch %2d, loss = %s» %(epoch, str(compute_loss(outputs, model(inputs)).numpy())))
- plt.legend()
- plt.draw()
- plt.ion()
- plt.pause(1)
- plt.close()
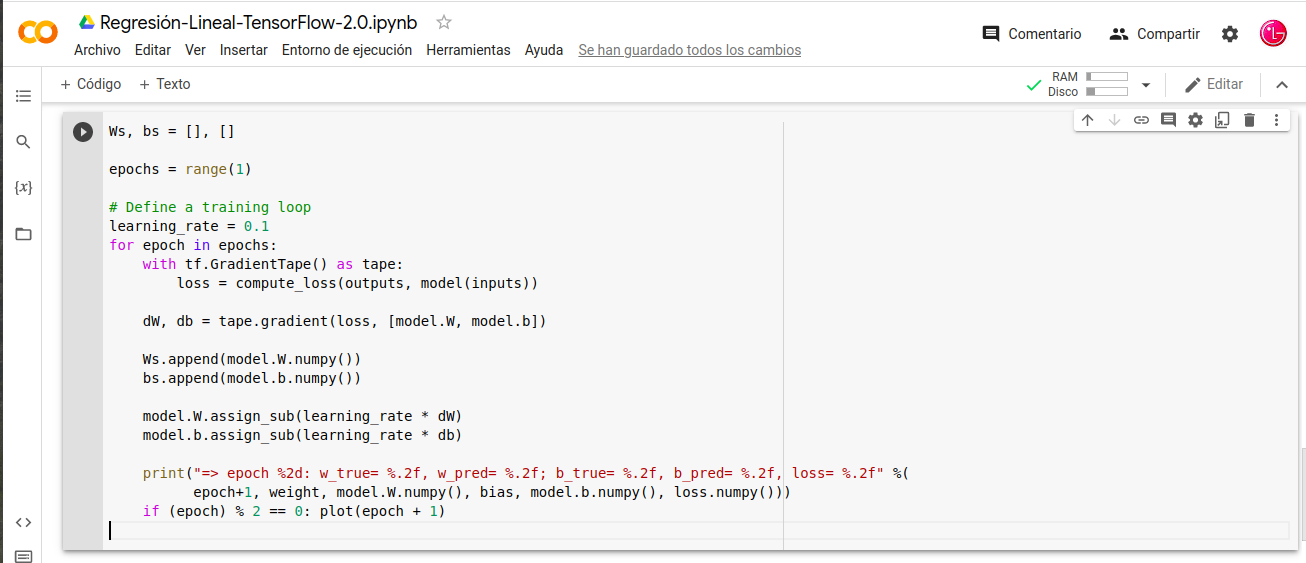
Modelo-Ejecutar-Entrenamiento:
- Ws, bs = [], []
- epochs = range(1)
- learning_rate = 0.1
- for epoch in epochs:
- with tf.GradientTape() as tape:
- loss = compute_loss(outputs, model(inputs))
- dW, db = tape.gradient(loss, [model.W, model.b])
- Ws.append(model.W.numpy())
- bs.append(model.b.numpy())
- model.W.assign_sub(learning_rate * dW)
- model.b.assign_sub(learning_rate * db)
- print(«=> epoch %2d: w_true= %.2f, w_pred= %.2f; b_true= %.2f, b_pred= %.2f, loss= %.2f» %(
- epoch+1, weight, model.W.numpy(), bias, model.b.numpy(), loss.numpy()))
- if (epoch) % 2 == 0: plot(epoch + 1)
Nota: Una época significa un paso completo del conjunto de datos de entrenamiento a través del algoritmo. El número de esta época es un hiperparámetro importante para el algoritmo. Especifica el número de épocas o pases completos de todo el conjunto de datos de entrenamiento que pasan por el proceso de entrenamiento o aprendizaje del algoritmo. En caso que nos ocupa he puesto 1 pero mal entrenamiento seria, lo normal seria 500,1000 son cantidades mas razonable.
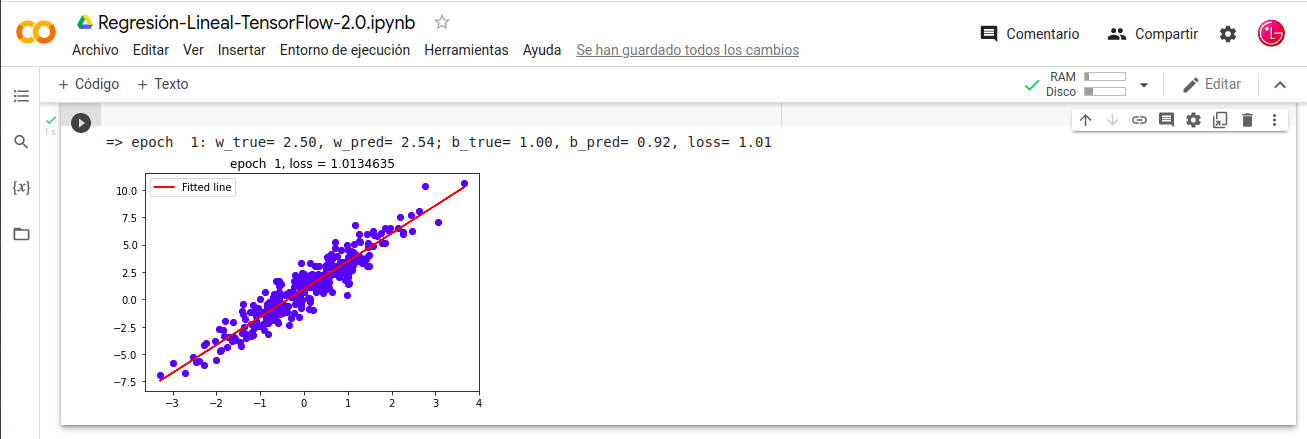
Nota: Se pueden crear gráficos de líneas para el proceso de entrenamiento, con el eje X teniendo la época en el aprendizaje automático y el eje Y teniendo la habilidad o el error del modelo. Dichos gráficos de líneas se denominan curva de aprendizaje del algoritmo y ayudan a diagnosticar problemas como el ajuste del conjunto de entrenamiento por debajo, por encima o adecuadamente aprendido. A continuación podemos visualizar el grafico de la curva de aprendizaje con 80 epochs.
Progreso-Entrenamiento-Modelo:
- plt.plot(epochs, Ws, ‘r’,
- epochs, bs, ‘b’)
- plt.plot([weight] * len(epochs), ‘r–‘,
- [bias] * len(epochs), ‘b–‘)
- plt.legend([‘W’, ‘b’, ‘true W’, ‘true_b’])
- plt.show()
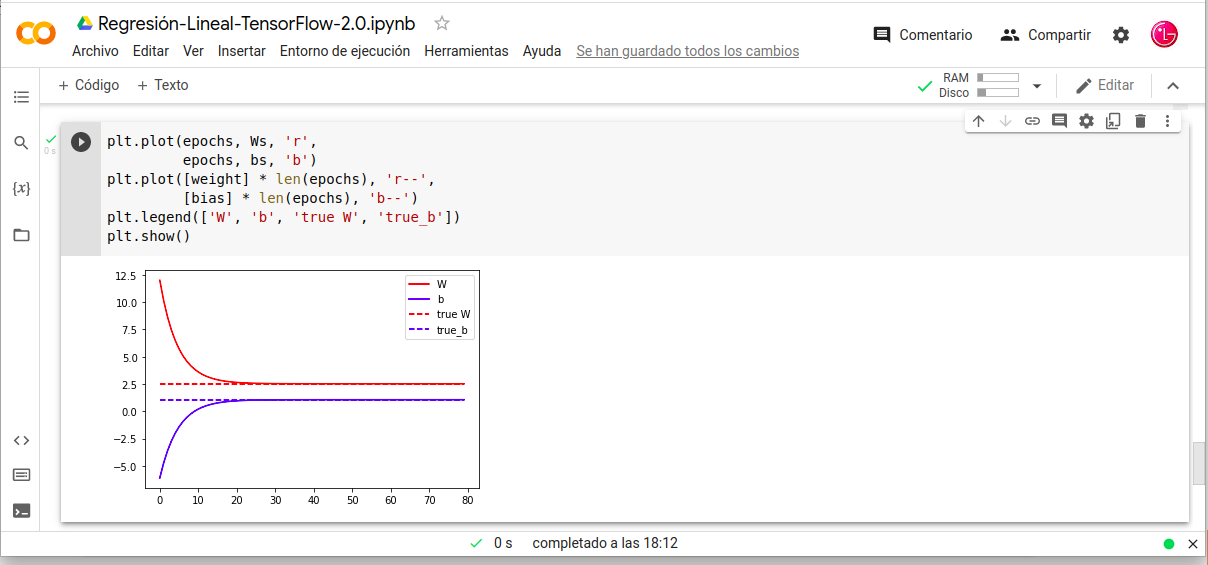
Nota: en este grafico nos muestra que partir de las 20-epochs se estabiliza con lo cual para su entrenamiento no necesitamos 80-epochs.
Recopilando:
En este post hemos puesto en escena la herramienta Google-Collaboration usando el Frameworks TensorFlow-2.0, con una Regresión-Lineal.
- Referencias: (Entorno-Moreluz)
- Referencias: TensorFlow

