Nota: (Los Perceptron-Multilayer MLP se inspiraron inicialmente en Perceptron , un algoritmo de aprendizaje automático supervisado para la clasificación binaria. El Perceptron solo era capaz de manejar datos linealmente separables, por lo que se introdujo la percepción de múltiples capas para superar esta limitación).
Perceptron-Multilayer (MLP)
-. Perceptron-Multilayer & Red-Neuronal-Artificial-Multicapa, es una red neuronal capaz de manejar datos separables tanto linealmente como no linealmente. Pertenece a una clase de redes neuronales conocidas como redes neuronales de avance, que conectan las neuronas en una capa con la siguiente capa de manera directa sin bucles.
-. Perceptron-Multilayer (MLP), es una red neuronal artificial y, por lo tanto, consta de neuronas interconectadas que procesan datos a través de tres o más capas. La estructura básica de un Perceptron-Multilayer (MLP) consta de una capa de entrada, una o más capas ocultas y una capa de salida, una función de activación y un conjunto de pesos y sesgos.
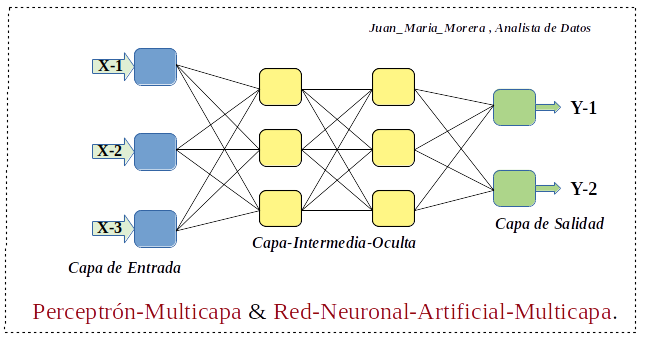
- Capa-Entrada: capa inicial de la red, tomando la entrada en forma de números
- Capa-Oculta-Intermedia: procesa la información recibida de la capa de entrada, es en forma de cálculos, sin restricción en la cantidad de capas ocultas.
- Capa-Salida: es responsable de producir resultados, es la salida de los cálculos aplicados a los datos a través de la red.
-. Perceptron-Multilayer (MLP), una de sus característica se encuentra en la Retropropagación , una técnica de Aprendizaje-Supervisado para entrenar una red neuronal. En términos simplificados, la Retropropagación es una forma de ajustar los Pesos en una red neuronal al propagar el Error desde la salida hacia la red Hacia-Atras. Esto mejora el rendimiento de la red al tiempo que reduce los Errores en la salida.
Nota: La Retropropagación se usa para hacer esos ajustes de ponderación y sesgo en relación con el error, y el error en sí se puede medir de varias maneras, incluido el error cuadrático medio (RMSE).
-. Perceptron-Multilayer (MLP), necesita tiempos de entrenamiento breves para aprender las representaciones en los datos y producir un resultado. Por lo general, también requerirían unidades informáticas más potentes que la computadora promedio. Un dispositivo con una Unidad de procesamiento seria uno de gráficos (GPU).
-. Perceptron-Multilayer (MLP), se usan para datos que no son separables linealmente, como el análisis de Regresión, son más adecuados para tareas complejas de clasificación y modelado predictivo.
- Utilizado para la Traducción-Automática.
- Utilizado para la Detección-Fraudes
- Utilizado para el Pronóstico-Tiempo
- Utilizado para la Predicción-Calificaciones-Crediticias
- Utilizado para la Predicción-Mercado-Valores.
Implementación-Perceptron-Multilayer-Scikit-Learn
-. Esta implementación no está pensada para aplicaciones a gran escala. En Scikit-Learn no ofrece soporte para GPU.
Nota: Usaremos el laboratorio Scikit-Learn / Jupyter-Notebook / Venv Entorno-Virtual-Python
-. Perceptron-Multilayer (MLP), es un algoritmo de aprendizaje supervisado que aprende una función entrenando en un conjunto de datos, don de es el número de dimensiones para la entrada y es el número de dimensiones para la salida. Dado un conjunto de características, un objetivo, puede aprender un aproximador de función no lineal para clasificación o regresión. Se diferencia de la regresión logística en que entre la capa de entrada y la de salida puede haber una o más capas no lineales, llamadas Capas-Ocultas.
Clasificación:
Class MLPClassifier implementa un algoritmo de Perceptrón–Multicapa (MLP) que entrena usando Backpropagation .MLP entrena en dos matrices: matriz X de tamaño (n_samples, n_features), que contiene las muestras de entrenamiento representadas como vectores de características de punto flotante; y matriz y de tamaño (n_samples), que contiene los valores objetivo (etiquetas de clase) para las muestras de entrenamiento.
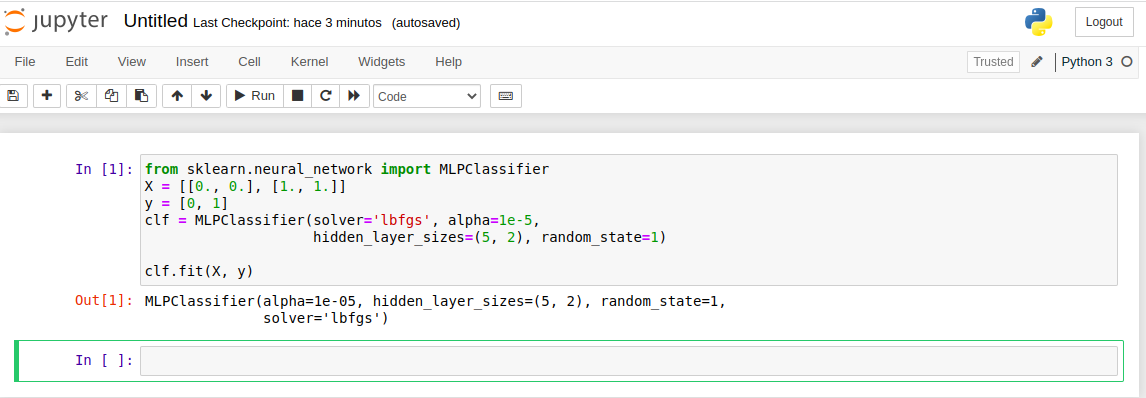
Nota: pegamos en nuestro Jupyter-Notebook la entrada (In) nos dará la salidad Out.
- In: from sklearn.neural_network import MLPClassifier
- In: X = [[0., 0.], [1., 1.]]
- In: y = [0, 1]
- In: clf = MLPClassifier(solver=‘lbfgs’, alpha=1e-5,
- hidden_layer_sizes=(5, 2), random_state=1)
- In: clf.fit(X, y)
- Out: MLPClassifier(alpha=1e-05, hidden_layer_sizes=(5, 2), random_state=1, solver=’lbfgs’)
Regresión:
Class MLPRegressor implementa un Perceptrón–Multicapa (MLP) que entrena usando Retropropagación sin función de activación en la capa de salida, que también puede verse como el uso de la función de identidad como función de activación. Por lo tanto, utiliza el Error-Cuadrático como Función de Pérdida y la salida es un conjunto de valores continuos.
Regularización:
Ambos MLPRegressor y MLPClassifierusan el parámetro alpha para el término de regularización (regularización L2) que ayuda a evitar el sobreajuste al penalizar los Pesos con grandes magnitudes.
Algoritmos:
Perceptrón–Multicapa (MLP) entrena usando Stochastic–Gradient–Descent (SGD) actualiza los parámetros utilizando el gradiente de la función de pérdida con respecto a un parámetro que necesita adaptación.
Nota: En esta Implementación he tomado como base la que encontramos en el docs de scikit-learn el cual tiene unos Tutoriales de scikit-learn muy recomendables scikit-learn.org
Recopilando:
Perceptron-Multilayer & Red-Neuronal-Artificial-Multicapa, es una red neuronal capaz de manejar datos separables tanto linealmente como no linealmente, el análisis de Regresión, son más adecuados para tareas complejas de clasificación y modelado predictivo; para este post he usado scikit-learn para su puesta en escena quizás tendría que usar Pytorch que tiene soporte mas adecuados como, CUDA , Computación de tensor, etc., lo dejare para cuando tratemos la librería PyTorch.
- Referencias: Entorno-Moreluz
- Referencias: Para-saber-mas
- Referencias: Scikit-Learn

