Nota: (A la salida de la neurona, puede existir, un filtro, función limitadora o umbral, que modifica el valor resultado o impone un límite que se debe sobrepasar para poder proseguir a otra neurona. Esta función se conoce como función de activación).
Función & Activación
En redes computacionales, la Función de Activación de un nodo define la salida de un nodo dada una entrada o un conjunto de entradas. Se podría decir que un circuito estándar de computador se comporta como una red digital de funciones de activación al activarse como «ON» (1) u «OFF» (0), dependiendo de la entrada. Esto es similar al funcionamiento de un Perceptrón en una Red neuronal artificial.
La función de activación devuelve una salida que será generada por la neurona dada una entrada o conjunto de entradas. Cada una de las capas que conforman la red neuronal tienen una función de activación que permitirá reconstruir o predecir. Además, se debe considerar que en la red neuronal se usará una función no lineal debido a que le permite al el modelo adaptarse para trabajar con la mayor cantidad de datos. Las funciones de activación se dividen en dos tipos como: lineal y no lineal.
Funciones de activación
- Función de activación lineal (conocida como identidad)
- Función de activación Sigmoidea (también conocida como función Logística )
- Función de activación Tangente hiperbólica , también conocida como Tanh
- Función de activación unidad lineal Rectificada (ReLU)
- Función de activación Softmax
- Función Unidad Lineal Exponencial ( ELU ) es una variación de ReLU
- Función de activación FugasReLU (Leaky ReLu)
- Función de activación (Swish) (Silbido)
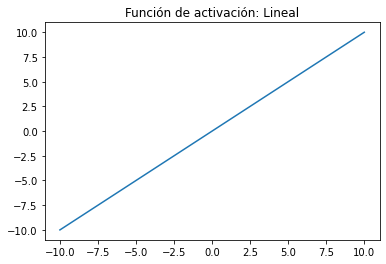
Función de activación lineal :
Una función de línea recta donde la activación es proporcional a la entrada (que es la suma ponderada de la neurona).Esta función también conocida como identidad, permite que lo de la entrada sea igual a la salida por lo que si tengo un red neuronal de varias capas y aplicó función lineal se dice que es una regresión lineal. Por lo tanto, esta función de activación lineal se usa si a la salida se requiere una regresión lineal y de esta manera a la red neuronal que se le aplica la función va a generar un valor único.
Ventajas :
- -. Proporciona una variedad de activaciones, por lo que no es una activación binaria.
- -. Definitivamente podemos conectar algunas neuronas juntas y si se dispara más de 1, podríamos tomar el máximo (o softmax) y decidir en base a eso.
Inconvenientes :
- -. Para esta función, la derivada es una constante. Eso significa que el gradiente no tiene relación con X.
- -. Es un gradiente constante y el descenso será en gradiente constante.
- -. Si hay un error en la predicción, los cambios realizados por la retropropagación son constantes y no dependen del cambio en la entrada delta (x).
Cargamos las bibliotecas :
- In: import numpy as np
- In: import matplotlib.pyplot as plt
- In: import numpy as np
- In: def linear(x):
- In: return x
- In: x = np.linspace(-10, 10)
- In: plt.plot(x, linear(x))
- In: plt.axis(‘tight’)
- In: plt.title(‘Función de activación: Lineal’)
- In: plt.show()
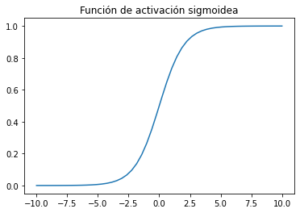
Función de activación Sigmoidea (también conocida como función Logística):
Sigmoide toma un valor real como entrada y genera otro valor entre 0 y 1. Es fácil de trabajar y tiene todas las propiedades agradables de las funciones de activación: es no lineal, continuamente diferenciable, monótona y tiene un rango de salida fijo.Para la función de activación en la red de aprendizaje profundo, la función sigmoide no se considera buena ya que cerca de los límites la red no aprende rápidamente. Esto se debe a que el gradiente es casi nulo cerca de los límites.
Ventajas :
- -. Es de naturaleza no lineal. ¡Las combinaciones de esta función también son no lineales!
- -. Dará una activación analógica a diferencia de la función de paso.
- -. También tiene un degradado suave.
- -. Es bueno para un clasificador.
-. La salida de la función de activación siempre estará en el rango (0,1) en comparación con (-inf, inf) de la función lineal. Entonces tenemos nuestras activaciones ligadas en un rango. Bien, entonces no volará las activaciones.
Inconvenientes :
- -. Hacia cualquier extremo de la función sigmoidea, los valores de Y tienden a responder mucho menos a los cambios en X.
- -. Da lugar a un problema de «gradientes que desaparecen».
- -. Su salida no está centrada en cero. Hace que las actualizaciones de gradiente vayan demasiado lejos en diferentes direcciones. 0 <salida <1, y dificulta la optimización.
- -. Los sigmoides saturan y matan los gradientes.
- -. La red se niega a aprender más o es drásticamente lenta (según el caso de uso y hasta que el gradiente / cálculo se ve afectado por los límites de valor de punto flotante).
- In: def sigmoid(x):
- In: return 1/(1+np.exp(-x))
- In: x = np.linspace(-10, 10)
- In: plt.plot(x, sigmoid(x))
- In: plt.axis(‘tight’)
- In: plt.title(‘Función de activación sigmoidea’)
- In: plt.show()
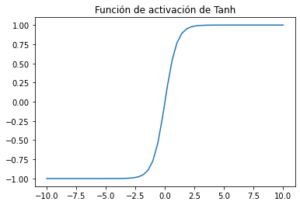
Función de activación Tangente hiperbólica , también conocida como Tanh:
Tanh aplasta un número real al rango [-1, 1] ( Tanh produce entre -1 y 1). No es lineal. Pero a diferencia de Sigmoid, su salida está centrada en cero. Por tanto, en la práctica siempre se prefiere la no linealidad tanh a la no linealidad sigmoidea.Tanh también sufre un problema de gradiente cerca de los límites al igual que la función de activación sigmoidea.
Ventajas :
- -. El gradiente es más fuerte para tanh que para sigmoide (las derivadas son más pronunciadas).
Inconvenientes :
- -. Tanh también tiene el problema de la desaparición del gradiente.
- In: def tanh(x):
- In: return np.tanh(x)
- In: x = np.linspace(-10, 10)
- In: plt.plot(x, tanh(x))
- In: plt.axis(‘tight’)
- In: plt.title(‘Función de activación de Tanh’)
- In: plt.show()
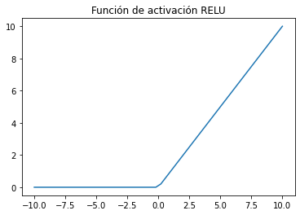
Función de activación unidad lineal rectificada (ReLU) :
RELU es una función de activación más conocida que se utiliza en las redes de aprendizaje profundo. RELU es menos costoso computacionalmente que las otras funciones de activación no lineal.
- -. RELU devuelve 0 si x (entrada) es menor que 0
- -. RELU devuelve x si x (entrada) es mayor que 0
Está función es la más utilizada debido a que permite el aprendizaje muy rápido en las redes neuronales. Si a esta función se le da valores de entrada muy negativos el resultado es cero pero si se le da valores positivos queda igual y además el gradiente de esta función será cero en el segundo cuadrante y uno en el primer cuadrante. Cuando se tiene que la función es igual a cero y su derivada también lo es se genera lo que es la muerte de neuronas, a pesar que puede ser un inconveniente en algunos casos permite la regularización Dropout. Por esta razón la función ReLu tiene una variante denominada Leaky ReLu que va a prevenir que existan neuronas muertas debido a la pequeña pendiente que existe cuando x<0. A pesar de su nombre y apariencia, no es lineal y proporciona los mismos beneficios que Sigmoid (es decir, la capacidad de aprender funciones no lineales), pero con un mejor rendimiento.
Ventajas :
- -. Evita y rectifica el problema de la desaparición del gradiente.
- -. ReLu es menos costoso computacionalmente que tanh y sigmoide porque involucra operaciones matemáticas más simples.
Inconvenientes :
- -. Una de sus limitaciones es que solo debe usarse dentro de capas ocultas de un modelo de red neuronal.
- -. Algunos gradientes pueden resultar frágiles durante el entrenamiento y pueden morir. Puede causar una actualización de peso que hará que nunca se active en ningún punto de datos nuevamente. En otras palabras, ReLu puede resultar en neuronas muertas.
- -. En otras palabras, para activaciones en la región (x <0) de ReLu, el gradiente será 0 debido a que los pesos no se ajustarán durante el descenso. Eso significa que las neuronas que entran en ese estado dejarán de responder a variaciones en el error / entrada (simplemente porque el gradiente es 0, nada cambia). A esto se le llama el problema de la muerte de ReLu.
- -. La gama de ReLu es [0,∞). Esto significa que puede hacer estallar la activación.
- In: def RELU(x):
- In: x1=[]
- In: for i in x:
- In: if i<0:
- In: x1.append(0)
- In: else:
- In: x1.append(i)
- In: return x1
- In: x = np.linspace(-10, 10)
- In: plt.plot(x, RELU(x))
- In: plt.axis(‘tight’)
- In: plt.title(‘Función de activación RELU’)
- In: plt.show()
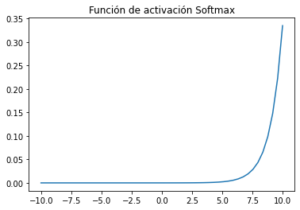
Función de activación Softmax :
La función Softmax calcula la distribución de probabilidades del evento sobre ‘n’ eventos diferentes. En general, esta función calculará las probabilidades de cada clase objetivo sobre todas las clases objetivo posibles. Posteriormente, las probabilidades calculadas serán útiles para determinar la clase objetivo para las entradas dadas. Softmax convierte logits, la salida numérica de la última capa lineal de una red neuronal de clasificación de clases múltiples en probabilidades.
- In: def softmax(x):
- In: return np.exp(x) / np.sum(np.exp(x), axis=0)
- In: x = np.linspace(-10, 10)
- In: plt.plot(x, softmax(x))
- In: plt.axis(‘tight‘)
- In: plt.title(‘Función de activación Softmax’)
- In: plt.show()
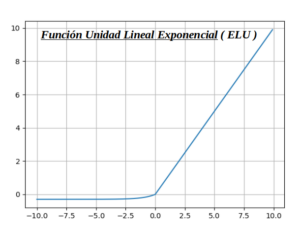
Función Unidad Lineal Exponencial ( ELU ) es una variación de ReLU :
Esta función de activación es una variante de ReLU que modifica la pendiente de la parte negativa de la función. A diferencia de Leaky ReLU y PReLU, en lugar de una línea recta, ELU usa una curva logarítmica para definir los valores negativos. ELU es una función que tiende a hacer converger el costo a cero más rápido y producir resultados más precisos. A diferencia de otras funciones de activación, ELU tiene una constante alfa adicional que debería ser un número positivo. ELU es muy similar a RELU excepto las entradas negativas. Ambos están en forma de función de identidad para entradas no negativas. Por otro lado, ELU se suaviza lentamente hasta que su salida es igual a -α, mientras que RELU se suaviza bruscamente.
Ventajas :
- -. ELU se suaviza lentamente hasta que su salida es igual a -α, mientras que RELU se suaviza bruscamente.
- -. ELU es una fuerte alternativa a ReLU.
- -. A diferencia de ReLU, ELU puede producir salidas negativas.
Inconvenientes :
- -. Para x> 0, puede aumentar la activación con el rango de salida de [0, inf].
- In: def elu(z,alpha):
- In: return z if z >= 0 else alpha*(e^z -1)
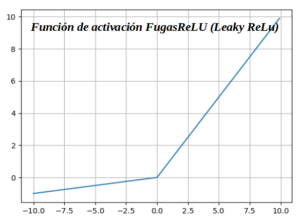
Función de activación FugasReLU (Leaky ReLu) :
Leaky ReLU es una mejora con respecto a la función de activación ReLU. Tiene todas las propiedades de ReLU, además, nunca tendrá el problema de ReLU moribundo. El concepto de ReLU con fugas es que cuando x <0, tendrá una pequeña pendiente positiva de 0,1. Esta función elimina de alguna manera el problema de la muerte de ReLU, pero los resultados obtenidos con ella no son consistentes. Aunque tiene todas las características de una función de activación de ReLU, es decir, computacionalmente eficiente, converge mucho más rápido, no se satura en la región positiva.
Ventajas :
- -. Los ReLU con fugas son un intento de solucionar el problema del «ReLU moribundo» al tener una pequeña pendiente negativa (de 0.01, más o menos).
Inconvenientes :
- -. Como posee linealidad, no se puede utilizar para la clasificación compleja. Se queda atrás de Sigmoid y Tanh para algunos de los casos de uso.
- In: def leakyrelu(z, alpha):
- In: return max(alpha * z, z)
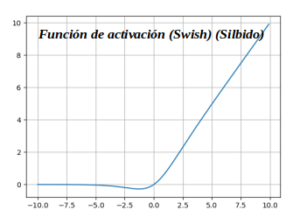
Función de activación (Swish) (Silbido) :
También conocida como función de activación autónoma, ha sido recientemente lanzada por investigadores de Google. La función de activación SWISH funciona mejor que ReLU, Podemos observar que en la región negativa del eje x la forma de la cola es diferente de la función de activación ReLU y debido a esto la salida de la función de activación Swish puede disminuir incluso cuando el valor de entrada aumenta. La mayoría de las funciones de activación son monótonas, es decir, su valor nunca disminuye a medida que aumenta la entrada. Swish tiene propiedad de delimitación unilateral en cero, es suave y no monótono.
- In: def swish(z):
- In: return z / (1 + np.exp(-z))
- In: swish(np.arange(-10, 10, 0.1))
Recopilando:
Con estos apuntes dan una visión de un conjunto de las Funciones de Activación, para las Neuronas Artificiales, colocadas en orden cronológico desde (Lineal) a la (Swish) .
- Referencias: Entorno-Moreluz
- Referencias: Para-saber-mas

